Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
septiembre 24, 2024
FRACCIONES DECIMALES Y CLASES DE DECIMALES
FUNCIONES
Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
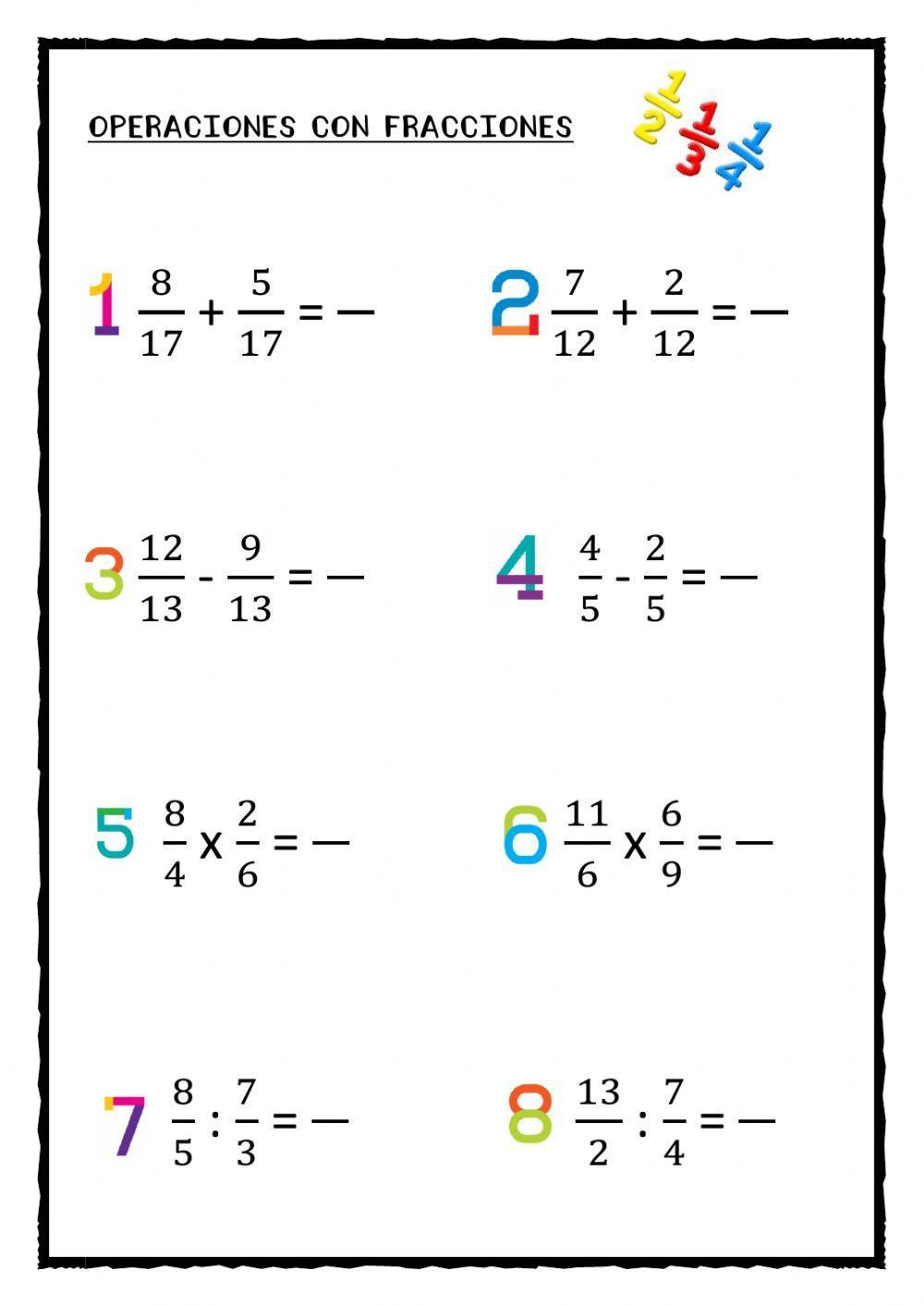
OPERACIONES ENTRE FRACCIONES
Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
BINOMIO AL CUBO
Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
Un binomio al cubo (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3
Ejemplo: (x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 =
= x 3 + 9x2 + 27x + 27
Ejercicios:
LA RECTA
Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
Partes de la Recta
- Puntos: Cualquier punto en la recta puede representarse mediante coordenadas en un plano cartesiano (x, y).
- Pendiente (m): Indica la inclinación de la recta. Se calcula como el cambio en y (vertical) dividido por el cambio en x (horizontal).
- Ordenada al origen (b): Es el punto donde la recta intersecta el eje y. Representa el valor de y cuando x es igual a 0.
Ecuaciones de la Recta
Ecuación General:
- Aquí, A, B y C son constantes. Esta forma es útil para determinar intersecciones con los ejes.
Ecuación de la Pendiente-Intersección:
- Donde m es la pendiente y b es la ordenada al origen. Esta forma es útil para graficar la recta.
Ejemplo:
Encuentra la ecuación de la recta que pasa por los puntos (2, 3) y (4, 7).
Calcular la pendiente (m):
Usar la forma pendiente-intersección:
- Usando el punto (2, 3):
El aprendizaje es un tesoro que nadie puede arrebatarte. ¡Gracias por permitirme ser parte de tu viaje! Nos vemos la próxima clase...💚
INTEGRALES PARTE I
Buenos días mis estudiantes, espero tengan un lindo día lleno de aprendizajes.
septiembre 23, 2024
34. PRÁCTICA EN MULTIPLICACIÓN POR FACTOR DE DOS CIFRAS
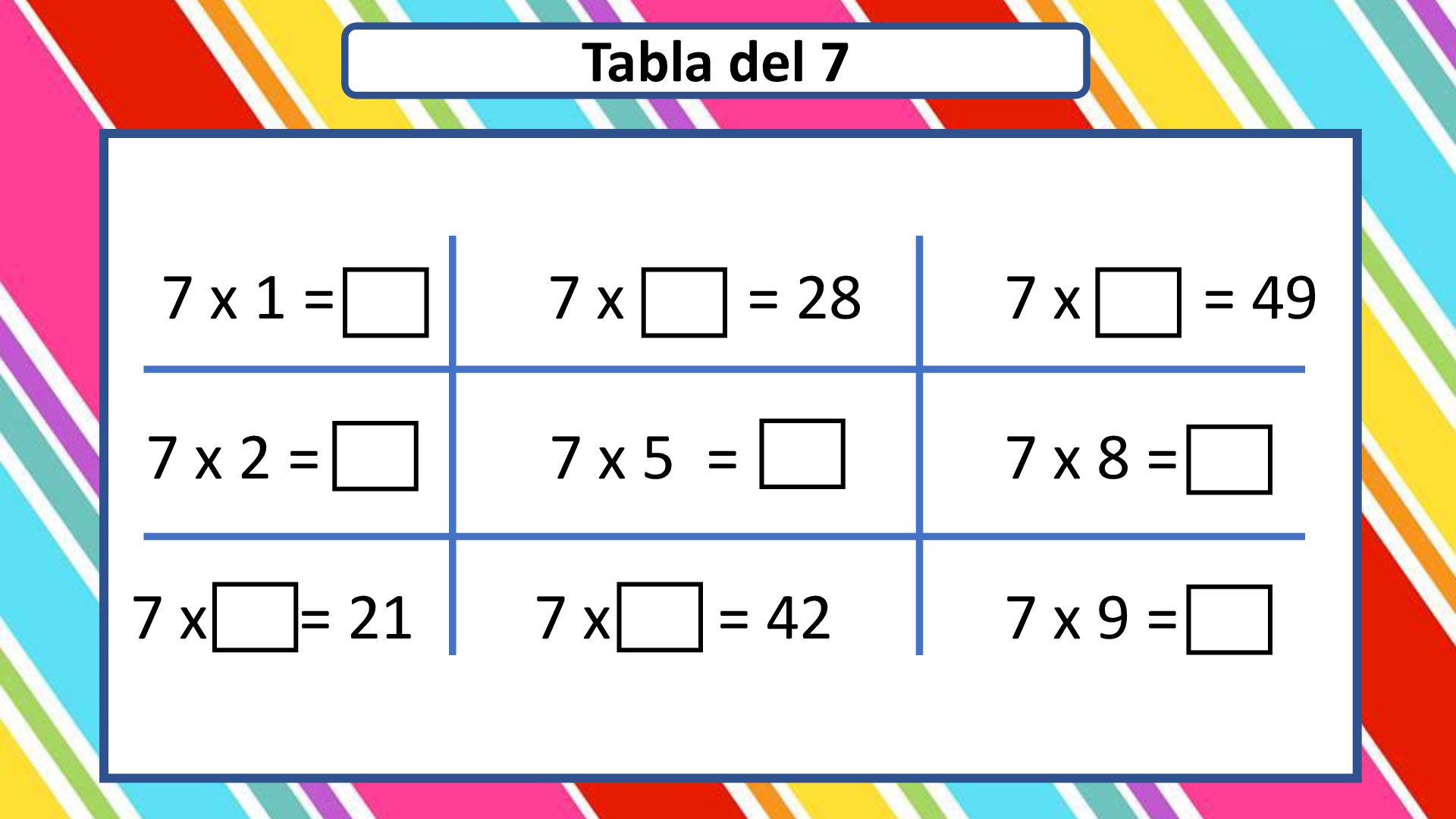
TABLA DEL 7.